Economic Section

Normal beam and column sections used in construction are rectangular or circular in reinforced concrete frames. But, it is noticed that the fibers near the neutral axis are understressed compared with those at top or bottom i.e., extreme end of section from neutral axis. The fact that a large portion of the cross section is thus understressed making it an inefficient for resisting flexure.

The flexure stress is derived by

α = (MC) / I

Where, I = moment of inertia of the desire section about a reference axis (neutral axis)

C = distance from the neutral axis to remotest fibers

M = resisting bending moment


α = flexural stress at remotest fiber.


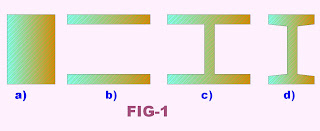If the area of a beam of rectangular section [fig-1(a)] is arranged so as to keep the same overall depth but have the shape shown in [fig-1(b)], the moment of inertia would be greatly increased, resulting in a greater moment resisting capacity. Actually, the increase in resisting moment is due to more fibers being located at a greater distance from the neutral axis. These fibers carry a greater stress and have a larger moment arm about the neutral axis to resist the applied bending moment. But, the section in [fig-1(b)] is not practical; the two parts of it would collapse together. It is necessary to use some of the area to fix these parts in place relative to each other, [fig-1(c)]. The web area transmits practically all the vertical shear.

[fig-1(c)] represents a wide-flange beam (referred to as a W shape). This is one of the most efficient structural shapes manufactured because it not only provides great flexural strength with minimum weight of material but is highly when used as a column. Another structural shape is the I beam (referred to as an S shape) in [fig-1(d)], it preceded the wide flange and because it is not so efficient has been largely replaced by the wide-flange beam.

Structural section should be such that resisting moment Mr = (αI)/c = αS must be equal to or greater the applied bending moment M.

That is

S ≥ M/ α

Where, S = section modulus of the selected section

The above equation indicates that a beam must be selected whose section modulus is equal to or greater than the ratio of bending moment to allowable stress.

The compression flanges of beams tend to buckle horizontally side sway if the beam is too long. This buckling is a column effect. When this lateral deflection is prevented by the floor system or by bracing the compression flanges at proper intervals, the full allowable stresses may be used. Otherwise, the stresses should be reduced.