Effective Span length: A structure is generally represented by a simple line diagram using a center line distances between column and between floor beams. But, In practical cases, the column may have considerable width as well as the beam may have considerable depth leaving some modification of the respective length of these members. As width and depth of column and beam respectively, is accounted in these center line diagram, the derived results (moment, shear, torsion etc.) due to self weight and superimposed loads, from analysis is not practical and reasonable one. These difference between their center line distances and clear distances raised concept of effective of effective span length which results in a practical substantially accurate value of the results.
It is usually assumed that the members are prismatic having constant moment of inertia between center
Significance of effective span length:In analysis of Beam as well as column the effective span length provides effective and sometimes economical results.
Beam Analysis
lines,but a beam intersecting a column have a moment of inertia about infinite between column face to column center line. This is due to the consideration that the depth of the beam greatly increased in that region. Thus consideration of actual variation in member depth in analysis produce increased support moment followed by decreased span moment. In addition, it is apparent that critical section for design for negative bending would be at the center line, through an effective depth of unlimited value is available, in the region of support, in the beam.
Column Analysis
The variation of width and moment of inertia stated above is also applicable for columns.
Nature of Variation
Beam
The slope of moment diagram for the beam is quite steep in the region of the support producing substantial difference between the support center line moment and face moment. If a section is designed considering center line moment, a unnecessary large section will result. It is economical also desirable to reduce support moments by elastic analysis to account for the finite width of the supports.
Effective span for simply supported and continuous beams are as follows:
1) Simply supported beams
The effective span of a simply supported beam shall be taken as the smaller of the distance between the centers of bearing, or the clear distance between supports plus the effective depth.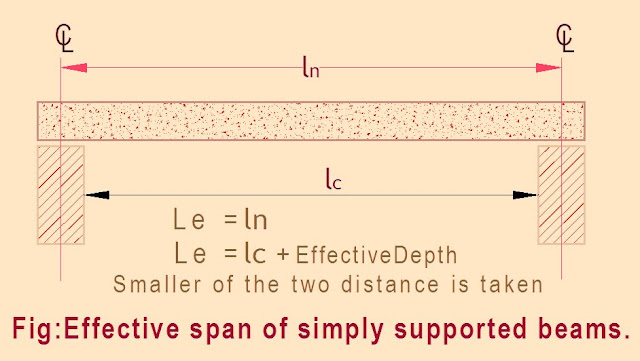
2) Continuous beams
If the width of support is less than 1/12 of the clear span, the effective span shall be taken as stated (1) above. If the supports are wider than 1/12 of the clear span or 600 mm, whichever is less, the effective span shall be as follows:
a) For end span with one fixed and the other continuous or for intermediate spans, the effective span shall be the clear span between supports.

b) For end span with one end free and other continuous, the effective span shall be equal to the clear span plus half the effective depth of the beam or the clear span plus half the width of the discontinuous support, whichever is less.
3) Monolithic frames
In case of monolithic frames, the effective span shall be equal to the distance between intersections of the center lines of the connecting members.
4) Cantilever beams
The effective length of the cantilever shall be taken as its length to the face of the supports plus half its effective depth except where it forms the end of a continuous beam where the length to the center of the support shall be used.

Column Analysis
The variation of width and moment of inertia stated above is also applicable for columns.
Nature of Variation
Beam
The slope of moment diagram for the beam is quite steep in the region of the support producing substantial difference between the support center line moment and face moment. If a section is designed considering center line moment, a unnecessary large section will result. It is economical also desirable to reduce support moments by elastic analysis to account for the finite width of the supports.
The difference in moment between support center line and support face is
equal to (Val)/3
Where , l=center line distance between support,
a l= column width
a= a ratio to column width to c/c distance between support.
Column
It is observed that,in the case of columns, the gradient of moment curve is not as steep as that for beam. So the difference between center line moment and the moment at the top and bottom face of the beam is small and in most cases it is disregarded.
Method of Approaches to analysis
Structural designers frequently uses two methods to analysis the frames. These are
1) The structure is simplified using simple line diagram and a deduction of (Val)/2 is done from center line moment without adjusting for the higher stiffness with in the thickness width of the column. This method is less realistic.
2) This involves the consideration of a rigid link within the width of the column, connecting the column center line with clear span of the flexural member. In case of column analysis, the portion of the column within the depth of the beam can also be represented using a rigid link. These is both realistic and easy to implement in matrix analysis programs.
Consequence of This Concept
Consequence of the concepts of effective span is reduction in congestion in the beam-column joint location where it is often difficult to place concrete because of the high quantity of reinforcing steel from the flexural members framing into the column (usually from two different directions) and from the column itself. But, a somewhat higher percentage of reinforcement required at midspan usually causes little difficulty in concrete placement.
equal to (Val)/3
Where , l=center line distance between support,
a l= column width
a= a ratio to column width to c/c distance between support.
Column
It is observed that,in the case of columns, the gradient of moment curve is not as steep as that for beam. So the difference between center line moment and the moment at the top and bottom face of the beam is small and in most cases it is disregarded.
Method of Approaches to analysis
Structural designers frequently uses two methods to analysis the frames. These are
1) The structure is simplified using simple line diagram and a deduction of (Val)/2 is done from center line moment without adjusting for the higher stiffness with in the thickness width of the column. This method is less realistic.
2) This involves the consideration of a rigid link within the width of the column, connecting the column center line with clear span of the flexural member. In case of column analysis, the portion of the column within the depth of the beam can also be represented using a rigid link. These is both realistic and easy to implement in matrix analysis programs.
Consequence of This Concept
Consequence of the concepts of effective span is reduction in congestion in the beam-column joint location where it is often difficult to place concrete because of the high quantity of reinforcing steel from the flexural members framing into the column (usually from two different directions) and from the column itself. But, a somewhat higher percentage of reinforcement required at midspan usually causes little difficulty in concrete placement.
Effective span for simply supported and continuous beams are as follows:
1) Simply supported beams
The effective span of a simply supported beam shall be taken as the smaller of the distance between the centers of bearing, or the clear distance between supports plus the effective depth.

2) Continuous beams
If the width of support is less than 1/12 of the clear span, the effective span shall be taken as stated (1) above. If the supports are wider than 1/12 of the clear span or 600 mm, whichever is less, the effective span shall be as follows:
a) For end span with one fixed and the other continuous or for intermediate spans, the effective span shall be the clear span between supports.

b) For end span with one end free and other continuous, the effective span shall be equal to the clear span plus half the effective depth of the beam or the clear span plus half the width of the discontinuous support, whichever is less.
3) Monolithic frames
In case of monolithic frames, the effective span shall be equal to the distance between intersections of the center lines of the connecting members.

4) Cantilever beams
The effective length of the cantilever shall be taken as its length to the face of the supports plus half its effective depth except where it forms the end of a continuous beam where the length to the center of the support shall be used.


THANKS
ReplyDelete